1. Алгебра
  2. Решите дана bn прогрессия

Решите дана bn прогрессия b3 ровно 1/25 b4=1/125 найти сумму первых 4 членов

abereziuk2017 abereziuk2017    1   21.07.2019 00:40    28

Ответы
ainashsharipov ainashsharipov  23.09.2020 01:15

Знаменатель геометрической прогрессии: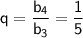 \sf q=\dfrac{b_4}{b_3}=\dfrac{1}{5}


По формуле n-го члена геометрической прогрессии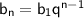 \sf b_n=b_1q^{n-1}, третий член:

\sf b_3=b_1q^2~~\Leftrightarrow~~ b_1=\dfrac{b_3}{q^2}=\dfrac{\dfrac{1}{25}}{\bigg(\dfrac{1}{5}\bigg)^2}=1



Сумма первых четырех членов геометрической прогрессии:

\sf S_4=\dfrac{b_1(1-q^4)}{1-q}=\dfrac{1\cdot\bigg(1-\bigg(\dfrac{1}{5}\bigg)^4\bigg)}{1-\dfrac{1}{5}}=\dfrac{5^4-1}{5^4-5^3}=\dfrac{(5^2-1)(5^2+1)}{5^3(5-1)}=\\ \\ \\ =\dfrac{(5-1)(5+1)(25+1)}{5^3\cdot(5-1)}=\dfrac{6\cdot26}{5^3}=\dfrac{156}{125}=1\dfrac{31}{125}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Xtanev Xtanev  25.09.2019 20:13
1) y=4x-132) промежутки моннотости f(x)=9x^2-36x3) найти нули функции y=12x-4x^24)f(x)=3x^2+2x^2-3 см пересдача...
1linia1 1linia1  25.09.2019 20:13
Отрезок, равный 17.6 см, разделен на 3 неравных отрезка. расстояние между серединами крайних отрезков равно 9.7 см. найдите длину среднего отрезка. . заранее !...
NastyaBelmesova NastyaBelmesova  25.09.2019 21:20
Решить систему уравнений 2x + 4/10= 1- 9(y-3)/20, 3y - 4/4= 9-x/3 -3/4...
olgavoronina19 olgavoronina19  25.09.2019 21:20
2x+7=-2x -5x=5x-6 -x-2=9x -6x-5=4x -x+7=6x решите...
Ася065 Ася065  25.09.2019 20:12
Следующие дроби к общему знаменателю 1)а/2x и b/4 ^3 2)3b и a^2/2b 3) b/3a , 3c/b2 и ab 4) 1/6b^2 , a^2+b^2/9a^2 b ^2 и 3-a^2/18ab^2...
leski leski  25.09.2019 21:20
Пассажирский поезд был задержан в пути на 16 мин и нагнал опоздание на перегоне в 80 км/ч, идя со скоростью на 10 км/ч большей, чем полагалось по расписанию. какова была скорость...
manokhaangel manokhaangel  02.03.2021 12:23
Продолжительность выполнения домашнего задания (в часах) по результатам опроса 10-ти учащихся приведена в виде ряда: 2,6 3,4 1,7 3,7 3,8 1,8 a) представьте данные в виле интервальной...
joje1 joje1  02.03.2021 12:23
Дана функция f(x) = 6x^2 + 3x -108 a) Найди значение функции f(3); b) Найди нули функции...
ПрикольнаяЖанеля ПрикольнаяЖанеля  02.03.2021 12:23
В треугольнике ABC известно, что AB=8, BC=8, AC=11. Найди cos∠ABC....
grasdas grasdas  02.08.2019 23:50
Как решить -2,4+35,05(1,4-0,9)= и 2 -- x 2,8-(5+143)= 5...

Популярные вопросы