Решите cos2xcosx=sin2xsinx должен получится такой ответ: x=п/6+nп/3, n є z
Ответы
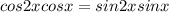
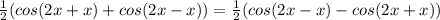
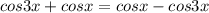
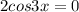
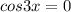
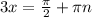
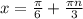 , где n - целые числа
, где n - целые числа
Другие вопросы по теме Алгебра
Популярные вопросы
- 1когда между однородными членами ставится запятая 2 как пишутся слова каждого...
3 - Объясните , что такое гипофиз + 5 примеров...
2 - Что такое тонус кровеносных сосудов?...
2 - Укажите верное определение параллели...
1 - Продолжи предложения из рассказа (горе от ума) 1)я 2)я считаю.. 3)меня привлекает...
1 - Густых елок - указать морфологические признаки...
2 - 3. не является отрезком речи а) морфема б) звук в) такт г) слог...
2 - Как можно использовать анимационные и звуковые эффекты в презентации?...
1 - −3,8(x−10)(x+2,7)=0 решите , скорее, за ранее...
3 - Составьте предложения с пятью водными словами!...
1