Решите через уравнение и с30

в двух мешках 150 кг муки. после того, как 1/8(дробь) часть муки из первого мешка переложили во второй, муки в мешках стало поровну. сколько было муки в каждом мешке изначально?
​

80 и 60 кг

Объяснение:

Пусть в 1-м мешке Х кг муки. Поскольку в двух мешках в сумме 140 кг, то на 2-й мешок приходится (140 - Х) кг муки. После того как восьмую часть муки переложили, в 1-м мешке останется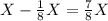 кг муки, а во 2-м станет 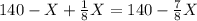. Поскольку муки в мешках стало поровну, приравняем данные выражения и составим уравнение:

В 1-м мешке изначально было 80 кг муки, значит во 2-м мешке её было 140 - 80 = 60 кг.