Решите биквадратные уравнения (x^2–16x)^2-2( x^2–16x)–63=0
(2x^2+3x)^2-7(2x^2+3x)+10=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Гемофилия - рецессивный признак, сцепленный с х - хромосомой. альбинизм - рецессивный...
3 - Сегодня надо ! 1. (3х+4)2(в квадрате) -(3х-1)(1+3х)=65 2.(2х-1)2(в квадрате) -...
3 - Найдите корень уравнения : х-4(9-х)=3х+2...
3 - 5предложений с описанием природы разобрать по членам и частям речи...
2 - Сколько кроссоверных и некроссоверных гамет будет образовывать дигетерозигота,...
1 - Корень третьей степени из x-2 = 2; корень третьей степени из 2x+7 = корень третьей...
1 - Осуществить превращения: а) cu- cuo- cuso4 - cu(oh)2- cuo. умоляю)!...
2 - Всодержащем разряженный газ при комнатной температуре, в 2 раза увеличили число...
2 - Решите неравенства 9x-11больше5(2х-3)...
1 - Можно ли сказать что личиночная жизнь организма является частью его индивидуального...
1
1.
Замена:
Получаем обычное квадратное уравнение:
Обратная замена:
1) При получаем:
получаем:
2) При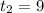 получаем:
получаем:
ответ: {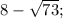
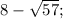
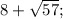
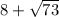 }
}
2.
1) При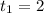
2) При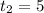
ответ: {-2,5; -2; 0,5; 1}