Решите алгебраическое выражение: 3/x-3 – x+15/x^2-9 – 1/x
Желательно с объяснением..
Другие вопросы по теме Алгебра
Популярные вопросы
- Расстояние между соседними гребнями волны на море равно 6 м . какова...
2 - Вгороде два овощных склада. по ошибке на один из них завезли в 4...
2 - Расстояние между равно 150 км. каким отрезком будет изображено это...
1 - Все тела 4.5 н,а его объём 500см^3.утонет ли это тело? a)в воде...
1 - Из 15м ткани сшили 10 платьев сколько платьев можно сшить из 3м...
1 - Может ли измениться жизнь под влиянием одного случая ? ? : после...
1 - Начерти незамкнутую ломаную из 6 звеньев так, чтобы длина каждого...
1 - Написати речення з двома підметами і двома присудками...
1 - Вырози в сантиметрах.6м=.2м8дм==.10м5дм4см=...
3 - Есть ли в комедии ревизор положительный герой?...
3
∅
Объяснение:
3/x-3 – x+15/x^2-9 – 1/x =
3/x - 3 - x + 15/(x-3)(x+3) - 1/x | * x * (x+3) =
(3x * (x+3) - x* (15 + x) - (x + 3)(x - 3)) / x * (x - 3) * (x + 3) =
(3x^2 + 9x - 15x - x^2 - x^2 + 9)/ x * (x - 3) * (x + 3) =
ОДЗ:
x * (x - 3) * (x + 3)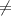 0
0
x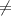 0; x
0; x 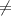 3; x
3; x 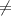 -3;
-3;
3x^2 + 9x - 15x - x^2 - x^2 + 9 =
x^2 - 6x + 9 = 0
x = 3
∅