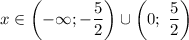Решите 4х^3 - 25x меньше 0
Другие вопросы по теме Алгебра
Популярные вопросы
- комектесндерш әдеби эссе жазп берндерш...
3 - Сумма углов треугольника на готовых чертежах. решить 15 и 13...
3 - To kin-sochinlik,ovunc,ahillik so zlari ishtirokida gaplar tuzingMavhum...
1 - У помідорів червоний колір забарвлення домінує над жовтим, а кругла форма...
1 - Что обьеденяет в раскрытии социального конфликта среди Тургенева,Лискова...
1 - по физике заполнить таблицу. Первую задачу я сделал, и заполнил 1 строку....
1 - ДАЮ Рассказ о с порте с местоимениями...
1 - Сөйлемдегі кейінді ықпалды сөзді тап: жұлдызшы, әлемін, аспан...
3 - Определяют не менее 3х основных последствий морских путешествий Чжэн Хэ;...
3 - 7. Какова трактовка темы маленького человека в романе Ф.М. Достоевского?...
3
ОДЗ: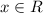
Найдем точки пересечения с осью абсцисс:
Нарисуем координатную прямую и отметим на ней точки пересечения с осью абсцисс, и найдем значение функции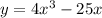 на каждом участке ("+" — если функция находится над осью абсцисс, "-" — если функция находится под осью абсцисс), подставляя в функцию число из промежутка (см. вложение).
на каждом участке ("+" — если функция находится над осью абсцисс, "-" — если функция находится под осью абсцисс), подставляя в функцию число из промежутка (см. вложение).
Так как у нас неравенство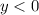 , то нас устроят промежутки со знаком "-", не включая точки пересечения с осью абсцисс.
, то нас устроят промежутки со знаком "-", не включая точки пересечения с осью абсцисс.
ответ: