Решите..........................................

ответ (6;5)

Для решение уравнения предлагаю следующий

Объяснение:

Введем целый коэффициент n такой, что .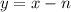

Выполним подстановку:

Упростим выражение:

Решим уравнение относительно x:

Тогда корни равны:

Очевидно, что уравнение имеет корни только, если

Найдем все такие целые n, при котором неравенство выполняется.

Решать будем так:

Заметим, что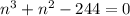 не имеет целых корней. Однако он больше 0, если 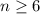и меньше 0, если 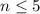(так как решаем в целых числах нам этого достаточно).

Если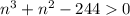 , то для того, чтобы неравенство выполнялось, 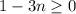, значит 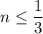, а так как решаем в целых числах, то можно написать 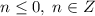. Найдем пересечение с 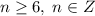и сделаем вывод, что такой случай невозможен.

Если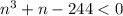 , то 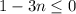, а значит 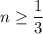, т.е. в нашем случае 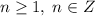. Найдем пересечение и сделаем вывод, что .

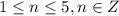Для каждого n найдем x и проверим будет ли он натуральным числом:

При n=1:

Здесь подходит только .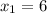

При этом x .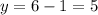

Получили пару чисел .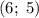

При n=2:

Ни один x не подходит.

При всех остальных n ни один x также не подходит.

Поэтому ответом будет являться .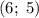

Задание выполнено!