решить задачу номер 1320 и 1322,
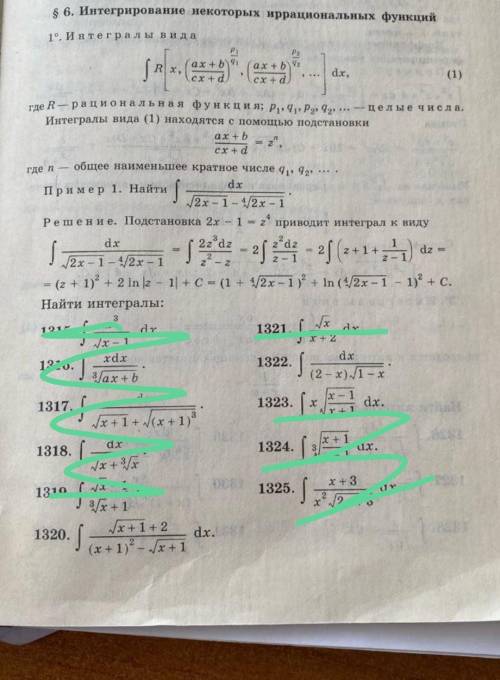
Другие вопросы по теме Алгебра
Популярные вопросы
- Поднятая проблема в фильме Два капина P. s. писать краткое содержание мне...
1 - Из прямоугольника со странами а=8см b=28см вырезали прямоугольник со сторонами...
1 - Найди значение буквенного выражения (с+36):5, при с = 264....
1 - Решите задания 5,6,7 как можно быстрее...
2 - Что больше всего дымит при горению...
2 - В 10 веке какие государства охватили все Азербайджанские земли ?...
2 - Катер по течению за 3 часа преодолел такое расстояние, как за 3 часа плывя...
3 - Определи какую окраску даёт тексту издревле ...
1 - Математика калаи шыгарады...
2 - Даны векторы a и b, и их модули |a| = 11 и |b|=6 . Если вектор c=a+b , то...
2
Раскладываем дробь на сумму простейших дробей методом неопределённых коэффициентов .