РЕШИТЬ ЗАДАЧУ! Найдите все натуральные числа, являющиеся решениями системы неравенств:
1)
{
{
2)
{
{
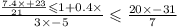
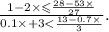
Другие вопросы по теме Алгебра
Популярные вопросы
- Мозговой штурм: ответьте устно на вопросы: 1 Что такое энергия? 2...
3 - K The Film I Have Recently WatchedRead the text. Choose the correct...
2 - Пароним к глаголу предоставляются (услуги)...
3 - Нужно решить первый пример...
1 - Give the singular of the following nouns: Exams,curricula,high,schools,lectures,students,subjects...
2 - При соединении треугольником Uфазное равно 220В, чему равно напряжение...
2 - Допишите уравнения предложенных реакции...
1 - с задачками по химии 1) Химическая термодинамика Сделать вывод о...
1 - Демографическая политика Определи рождаемость в государстве N за...
2 - Напишите какое значения имееют данные сочетания и выражения. Сансыз...
2
Первая система - 1-2 фото, вторая 3-5
Натуральными числами, являющимися решениями первой системы будут числа 2,3,4
Натуральными числами, являющимися решениями второй системы будут числа 1, 2, 3
В решении.
Объяснение:
Решить систему неравенств:
1) (7,4х + 23)/21 <= 1 + 0,4x
3x - 5 <= (20x - 31)/7
Умножить обе части первого неравенства на 21, а второго на 7, чтобы избавиться от дробного выражения:
7,4х + 23 <= 21(1 + 0,4x)
7(3x - 5) <= 20x - 31
Раскрыть скобки:
7,4x + 23 <= 21 + 8,4x
21x - 35 <= 20x - 31
7,4x - 8,4x <= 21 - 23
21x - 20x <= -31 + 35
-x <= -2
x <= 4
x >= 2 (знак неравенства меняется при делении на -1)
x <= 4
Решение первого неравенства х∈[2; +∞);
Решение второго неравенства х∈(-∞; 4];
Решение системы неравенств [2; 4], пересечение.
Неравенства нестрогие, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
Натуральные числа: 2; 3; 4 (2 и 4 входят в решения системы).
2) 1 - 2х <= (28 - 53x)/27
0,1x + 3 < (13 - 0,7x)/3
Умножить обе части первого неравенства на 27, а второго на 3, чтобы избавиться от дробного выражения:
27(1 - 2х) <= 28 - 53x
3(0,1x + 3) < 13 - 0,7x
Раскрыть скобки:
27 - 54х <= 28 - 53x
0,3x + 9 < 13 - 0,7x
-54x + 53x <= 28 - 27
0,3x + 0,7x < 13 - 9
-x <= 1
x < 4
x >= -1 (знак неравенства меняется при делении на -1)
x < 4
Решение первого неравенства х∈[-1; +∞);
Решение второго неравенства х∈(-∞; 4);
Решение системы неравенств [-1; 4), пересечение.
Первое неравенство нестрогое, скобка квадратная, второе - строгое, скобка круглая, а знаки бесконечности всегда с круглой скобкой.
Натуральные числа: 1; 2; 3 (4 не входит в решения системы).