Решить задачи по готовым чертежам.
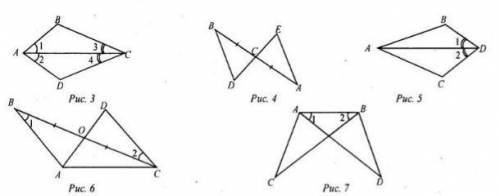
1) На рис. 3 ∠1 = ∠2 и ∠3 = ∠4. Докажите, что ΔАВС = ΔADC.
2) На рис. 4 АС = СВ, ∠A = ∠B. Докажите, что ΔBCD = ΔАСЕ.
3) На рис. 5 AD - биссектриса угла ВАС, ∠1 = ∠2. Докажите, что ΔABD = ΔACD.
4) На рис. 6 ВО = ОС, ∠1 = ∠2. Укажите равные треугольники на этом рисунке.
5) На рис. 7 ∠1 = ∠2, ∠CAB = ∠DBA. Укажите равные треугольники на это
Другие вопросы по теме Алгебра
Популярные вопросы
- Презентация на тему Неон Ne10 химический элемент...
3 - Написати твір Які 3 твори мені найбільше сподобалися з української...
3 - точка S віддалена від площини трикутника ABC на корінь(7) см і рівновіддалена...
2 - Розв язати систему,яка складається з рівнянь: 2x+3y=7 i -5x+2y=11У...
1 - Презентация на тему Финансовой рынок. Как он работать До 9строниц...
1 - Встановіть відповідь самостьйна робота 6 клас по біології...
3 - Розв яжи рівняння x - 7/19 = 3/19 і 5/19 - x =2/19...
2 - Если в двойной цепи В-ДНК 600 дезоксириб, сколько нуклеотидов РНК...
3 - У турнірі першості з футболу брало участь 17 команд. Кожна команда...
3 - Освободитесь от иррациональности в знаменателе...
3
1) дано: ∠1 = ∠2,∠3 = ∠4
доказать: ΔАВС=ΔADС
доказательство:
ΔАВС=ΔADС (по первому признаку)
∠1 =∠2
∠3 =∠4
АС=АС (общая)
ответ:ΔАВС=ΔADС
2) дано: АС = СВ, ∠A = ∠B
доказать: ΔBCD = ΔАСЕ
доказательство:
ΔBCD = ΔАСЕ (по первому признаку)
АС = СВ
∠A = ∠B
ответ: ΔBCD = ΔАСЕ
3) дано: AD - биссектриса угла ВАС, ∠1 = ∠2
доказать:ΔABD = ΔACD
доказательство:
ΔABD = ΔACD (по 1му признаку)
AD - биссектриса угла ВАС
∠1 = ∠2
АD- общая
ответ: ΔABD = ΔACD
4) дано: ВО = ОС, ∠1 = ∠2
доказать: АВО и ОDС- равные
доказательство:
ΔАВО=ΔОDС (по 1му признаку)
ВО = ОС
∠1 = ∠2
ВС=ВС- общая
АО=ОD
ВА=DC
ответ: равные треугольники это: ΔАВО и ΔОDС
5) дано: ∠1 = ∠2, ∠CAB = ∠DBA
доказать: ΔАВD=ΔBAC
доказательство:
ΔАВD=ΔBA (по 1му признаку)
∠1 = ∠2
∠CAB=∠DBA
АD=BC
ответ: равные треугольники это: ΔАВD и ΔСBA