Решить возвести в степень и вычислить

Объяснение:

Итак, вспоминаем алгебру 7-го класса.

Для того, чтобы перемножить алгебраические дроби, необходимо разложить на множители числитель и знаменатель. Благо, раскладывать на множители нам надо только в числителе второй дроби. Мы видим, что a² - n² - это формула разности квадратов(формулы сокращенного умножения надо выучить, иначе ты не сможешь осилить дальнейший курс алгебры!). Раскладываем формулу: (a - n)(a + n).

Получаем дроби:

3 в числителе первой дроби и 3 в знаменателе второй дроби сократятся, (a + n) в числителе второй дроби и (a + n) в знаменателе первой дроби сократятся.

Останется:

№2.

(a + x) *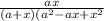

Обрати внимание: мы в знаменателе второй дроби раскрыли формулу, которая называется сумма кубов(выучи формулы сокращенного умножения!).

(a + x) сократится, останется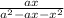

№3.

Опять же, вспомним алгебру 7 класса, а именно свойства степеней.

Нам нужно одно свойство степеней, а именно:

Формулируем свойство: если нам требуется возвести дробь в энную степень, то в эту энную степень возводится и числитель и знаменатель.

Воспользуемся этим:

xc возводим в пятую степень:

x^5c^5

(^5 - это степень)

Возводим знаменатель в степень:

a^5y^5(c+x)^5

ответ: x^5c^5/a^5y^5(c+x)^5