Решить! в арифметической прогрессии а1=75 [а1=-40] d=-3 [d=4/5] найдите шестой член прогрессии и сумму первых шести членов этой прогрессии

Ответы

Владуся28 01.10.2020 15:59

a_n=a_1+(n-1)d — n-ый член арифметической прогрессии

$S_n=\dfrac{a_1+a_n}{2}\cdot n$ — сумма n первых членов а.п.

1)~a_1=75;~~ d=-3

Шестой член арифметической прогрессии:

$a_6=a_1+(6-1)d=a_1+5d=75+5\cdot(-3)=75-15=60$

Сумма первых шести членов этой прогрессии:

$S_6=\dfrac{a_1+a_6}{2}\cdot 6=\dfrac{75+60}{2}\cdot6=405$

2) Аналогично, для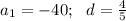 $a_1=-40;~~ d=\frac{4}{5}$

$a_6=a_1+5d=-40+5\cdot\frac{4}{5}=-40+4=-36$

$S_6=\dfrac{a_1+a_6}{2}\cdot 6=3\cdot(-40-36)=-228$

ПОКАЗАТЬ ОТВЕТЫ

вкпа 15.01.2024 14:35

Добрый день! Разберем задачу по частям.

В данной арифметической прогрессии мы имеем заданные значения первого члена (а1) и разности (d). Нам нужно найти значение шестого члена прогрессии и сумму первых шести членов.

1. Найдем шестой член прогрессии.

Для этого используем формулу общего члена арифметической прогрессии:

an = a1 + (n-1)d,

где an - нужный нам член прогрессии,
a1 - первый член прогрессии,
n - номер этого члена в прогрессии,
d - разность.

В первом варианте прогрессии, где a1 = 75 и d = -3, получаем:

a6 = 75 + (6-1)(-3),
a6 = 75 + 5(-3),
a6 = 75 - 15,
a6 = 60.

Во втором варианте прогрессии, где a1 = -40 и d = 4/5, получаем:

a6 = -40 + (6-1)(4/5),
a6 = -40 + 5(4/5),
a6 = -40 + 4,
a6 = -36.

Таким образом, в обоих вариантах шестой член прогрессии равен:

a6 = 60 (для арифметической прогрессии с a1 = 75 и d = -3),
a6 = -36 (для арифметической прогрессии с a1 = -40 и d = 4/5).

2. Найдем сумму первых шести членов прогрессии.

Для этого воспользуемся формулой суммы первых n членов арифметической прогрессии:

Sn = (n/2)(a1 + an).

В первом варианте прогрессии, где a1 = 75, d = -3 и n = 6, получаем:

S6 = (6/2)(75 + 60),
S6 = 3(135),
S6 = 405.

Во втором варианте прогрессии, где a1 = -40, d = 4/5 и n = 6, получаем:

S6 = (6/2)(-40 + (-36)),
S6 = 3(-76),
S6 = -228.

Таким образом, в обоих вариантах сумма первых шести членов прогрессии равна:

S6 = 405 (для арифметической прогрессии с a1 = 75, d = -3),
S6 = -228 (для арифметической прогрессии с a1 = -40, d = 4/5).

Надеюсь, эта подробная информация помогла вам понять, как решить задачу. Если остались вопросы, пожалуйста, задавайте!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра