Решить уравнения а) (1+корень из 2 cos(x+п/ x - 3) = 0 б) 2 sin x/2 cos x/2 = cosx/2
Ответы
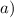
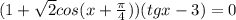
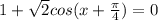 или
или 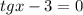
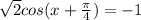 или
или 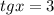
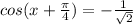 или
или 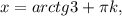
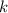 ∈
∈ 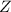
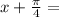 ±
± 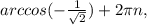
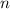 ∈
∈ 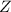
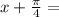 ±
± 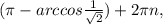
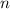 ∈
∈ 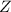
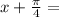 ±
± 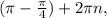
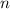 ∈
∈ 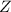
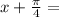 ±
± 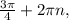
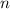 ∈
∈ 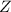
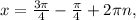
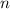 ∈
∈ 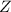 или
или 
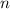 ∈
∈ 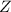
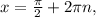
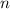 ∈
∈ 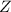 или
или 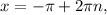
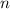 ∈
∈ 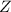
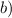
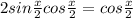
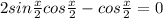
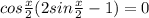
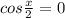 или
или 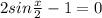
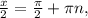
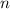 ∈
∈ 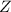 или
или 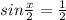
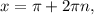
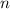 ∈
∈ 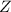 или
или 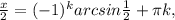
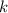 ∈
∈ 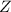
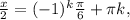
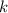 ∈
∈ 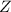
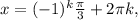
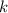 ∈
∈ 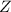
Другие вопросы по теме Алгебра
Популярные вопросы
- Русский язык : упражнение 4А четвёртое предложение выписать, от туда два глагола...
3 - 4-тапсырма. Берілген сөйлемге фонетикалық талдау жасаңдар. Ежелгі түркілердің жазу...
3 - Put the following words to make questions. (Расставь слова так, чтобы получились...
3 - (1:0.3-2 1/2)*2 1/7решить уравнение...
2 - 1. Посмотрите по карте и постарайтесь ответить на вопрос: почему значительная часть...
3 - Решение уравнения (22-25) 2) -(х²-2) - 0,3+7х+(х²-0,2х)=0...
2 - Рассуждение этого предложения минимум 5 предложений Русский язык в умелых руках...
1 - ‼️самостоятельная работа. тема: Мифы Древней Греции. Задание: Подготовить сообщение...
3 - Какие моря и океаны омывают россию...
1 - 11. Write the plurals. 1.Cap Two caps 2. Watch two 3. Fish two 4 Bus two 5. Tomato...
3