Решить уравнения: 1)3sin²2x+7cos2x-3=0; 2)sinx-cosx=0; 3)sinx-cos3x=0; 4)cosx-sinx=1.
Другие вопросы по теме Алгебра
Популярные вопросы
- Вбиблиотеку 96 тетрадей. их распределили для шести классов поравну. сколько...
3 - Що означає фразеологізм памороки забило?...
2 - Аразве дети выросли это словосочетание?...
1 - Расставте знаки препинания и объясните...
2 - Составить одно предложение со словом тым ақылды...
1 - Разобрать по членам, надписать части речи, у существительных определить...
3 - Вычислите значение выражения: 1)1,29: 4,3+18: 0,15+9: 45-1,4: 0,35=...
2 - Умаши и тани вместе 1037 марок. у маши на 133 марки больше, чем у тани....
1 - Напишите диалог 6 реплик на румынском языке на тему : у врача ! )...
3 - Вчём разница между праздный и праздничный...
1
1)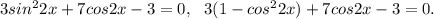
cos2x = 0
x = pi/4 + pik/2, k: Z.
2) Поделив на cosx:
tgx = 1
x = pi/4 + pik, k: Z.
3) Воспользуемся формулой приведения:
cos(pi/2 -x) - cos3x = 0
2sin(pi/4 +x)sin(2x-pi/4) = 0
sin(pi/4 +x) = 0 sin(2x-pi/4) = 0
x = -pi/4 + pi*k x = pi/8 + pi*k/2, k: Z
4) sinx - cosx = -1