Решить уравнение.
(x-6)^4+(x-4)^2=82
Другие вопросы по теме Алгебра
Популярные вопросы
- Турист приближается к национальной библиотеке на расстояние s = 120 м...
2 - Яких іноземних загарбників перемогли карпатьські українці герої повісті...
2 - Моторний човен пропливає річкою від селища а до селища б за дві години...
1 - 11,2л (н.у.) оксида азота (iv) и кислорода равными мольными долями пропустили...
2 - Р.и. фраерман девочка с камнем. определи, этот текст - описание,повествование...
3 - Когда надо вынести за скобки общий множитель, например тут: 8x - 24 надо...
1 - Докажите или опровергните, что послевоенные годы стали апогеем сталинизма....
1 - Написать сочинение на тему: обычаи моей местности (новый год , колядки...
2 - Меня учитель кинет через прогиб...
1 - Спишите,расставляя недостающие знаки препинания,вставляя, где нужно,пропущенные...
3
Думаю, что в уравнении ошибка, т.к. имеется еще один корень - корень уравнения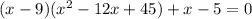 ; Для полноты напишу его (можно использовать формулу Кардано):
; Для полноты напишу его (можно использовать формулу Кардано):