1. Алгебра
  2. Решить уравнение x^2=(9x-22)^2​

Решить уравнение x^2=(9x-22)^2​

atrocities22 atrocities22    2   29.10.2020 20:56    0

Ответы
nastiatsiupak nastiatsiupak  28.11.2020 20:57

x^{2} = (9x-22)^{2}

Разложим:

x^{2} = 81x^{2} - 396x + 484

Переносим слагаемое в левую часть:

x^{2} - 81x^{2} + 396x - 484=0

Приводим под. члены:

-80x^{2} +396x -484 =0

Делим обе стороны на -4 (Для удобства дальнейших вычислений):

20x^{2} -99x+121=0

Раскладываем на множители:

20x^{2} - 44x - 55x + 121 =0\\

Раскладываем опять на множители:

4x*(5x-11) - 11(5x-11)= 0

Раскладываем вновь на множители:

(5x-11)*(4x-11)= 0

Тут будет два случая, или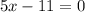 5x-11= 0

                                      или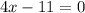  4x-11=0

Решаем и получаем в 1-ом уравнении: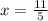 x=\frac{11}{5}

Во 2-ом уравнении выходит: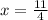 x=\frac{11}{4}

ответ: x1 = 2,2; x2 = 2,75. (Как два решения уравнения)

Прости, за долгое ожидание, т.к. заморачивалась с оформлением

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
yana3657 yana3657  25.12.2020 07:21
Функция задана формулой y=4x-30. Определите: а) значение y, если x= -1,5; б) значение x, при котором y= -5; в) проходит ли график функции через точку B(7;-3)....
105184 105184  25.12.2020 07:21
Преобразуйте уравнение 〖(х-2)〗^2=3х(х-1) к виду ax^2+bx+c=укажите старший коэффициент, второй коэффициент и свободный член....
мурgsng мурgsng  25.12.2020 07:21
1. Найдите периметр треугольника, если его стороны выражены многочленами а=ху³, b=3xy³+6x-4y, c=2xy³+2x, ответ запишите виде многочлена стандартного вида и укажите...
olyakak00Fokcu olyakak00Fokcu  25.12.2020 07:22
Найдите значение коэффициента k если известно что график функции у=k/x проходит через точку с координатами А(-3;-1) А)3В)1С)-1D)-3​...
СашаСтоляров1 СашаСтоляров1  25.12.2020 07:22
Дана арифметическая прогрессия (an): a1 = -11, d = 6. b) найди сумму первых шести членов данной прогрессии.​...
kattun kattun  25.12.2020 07:23
Моторная лодка км по течению реки и 70 км против течение реки, затратив на весь путь 10 часов. Найдите собственную скорость лодки, если скорость течение реки 2км/ч....
дияр22 дияр22  25.12.2020 07:23
Решить с полного квадрата с полным решением x в четвёртой степени + 2x в квадрате + 1 25a в квадрате + 10ab + 4bв квадрате x в квадрате - 19x - 45...
Екатерина21082006 Екатерина21082006  25.12.2020 07:23
Поясните как получилось (х²-4х+3) И как от всего этого получилось 3х²+4х-3=0...
Керис Керис  04.06.2019 09:40
Пусть d36 множество всех натуральных делителей числа 36, а d45 множество всех натуральных делителей числа 45. найти множество d36 ∩d45...
катя10467743 катя10467743  04.06.2019 09:40
X(x-7)=8 решить уравнение.у меня есть ответ.его просто нужно проверить...

Популярные вопросы