решить уравнение, только можно подробнее
Уравнение ниже прикрепила
Другие вопросы по теме Алгебра
Популярные вопросы
- Формула борной кислоты н3во3. укажите состав ее молекулы?...
1 - Используйте буквы, чтобы сформировать глаголы ksa. hares. ysa .kolo....
3 - Сколько будет в процентах три минуты от часа ?...
3 - Вкакой четверти числовой окружности находится точка : а)-2; б)-4;...
2 - 3(степень) корня9 умножить 8(степень) корня9...
1 - Тело набывает позитивного заряда в случае: а)утраты електронов б)присойденения...
3 - Карлсон съел 1/2 всех пирожных и ещё два, малыш-1/8 всех пирожных...
3 - Почему варварские королевства называют варварскими (не пишите ,...
2 - По каким признакам можно определить волшебную сказку? выбери словосочитания...
3 - Что воспевает пушкин в песне о вещем олеге...
2
0;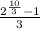
Объяснение: