Решить уравнение

Область значений функции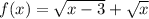 это 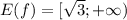, поскольку функция является возрастающей, как сумма двух возрастающих функций и минимум функции будет в точке x = 3.

- парабола, ветви которой направлены вниз. Найдем координаты вершины параболы

Поскольку на промежутке x ∈ [-3;+∞) функция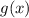 убывает и на промежутке x ∈ [√3;+∞) функция 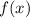возрастает. Значит, уравнение f(x)=g(x) имеет не более одного корня. х = 4 - корень уравнения

ответ: х = 4.