Решить уравнение sin^20(x)+cos^13(x)=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Дан равнобедренный треугольник с боковой стороной BC=4см и с медианой опущенной...
2 - Use -er/-or to complete the nouns.Check your spelling...
2 - Какие продукты делают из нас пассивным курильщиков ?...
2 - Кто из альтернативы6 класс 3...
1 - Листопад что сделал? 2 слова...
2 - Синоніми до слова горизонт...
2 - ів ПРИРОДНІ СИМВОЛИ УКРАЇНИ Символами країни, народу можуть бути природні об єкти....
2 - Sin^4(x)+cos^4(x)=cos^2(2x) решите неравенство ответ с объяснением...
2 - Випишіть прості речення. Підкресліть у них члени речення. Обгрунтуй те свій вибір....
2 - Английский язык 5 класс рабочая тетрадь страница 4 номер 1...
2
Поскольку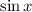 и
и 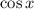 не превышают единицы по модулю, то для любых натуральных
не превышают единицы по модулю, то для любых натуральных 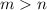 верно
верно 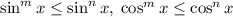 . Поэтому
. Поэтому 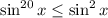 ,
, 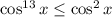 . Складывая оба неравенства, получаем
. Складывая оба неравенства, получаем 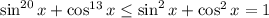 с равенством тогда и только тогда, когда или синус (или косинус) равен нулю, а косинус (или синус +-1) равен 1. Итак, решения следующие:
с равенством тогда и только тогда, когда или синус (или косинус) равен нулю, а косинус (или синус +-1) равен 1. Итак, решения следующие: 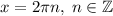 ,
, 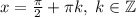 .
.