решить уравнение с заменой неизвестного /8кл

Популярные вопросы
- 2). Сравните географическое положение Финляндии и Дании, Швеции и Норвегии,...
1 - У людини карий колір очей домінує над голубим. Кароока жінка, в батька якої...
3 - В летнем лагере Кенгуру было предложено 10 задач. За каждый правильный ответ...
3 - Из пункта А в пункт В отправился велосипедист со скоростью 15 км/ч. Спустя...
2 - решить один пример по тригонометрии...
1 - что было розписанно все три задание...
1 - Лист улюбленому персонажу твору Лесі Ворониної Таємне Товариство Боягузів десь...
2 - Максим хочет составить квадрат из одинакового количества квадратиков со стороной...
3 - 1.Как можно охарактеризовать ритм в стихотворении О как безумно за окном?2.В...
1 - ДОМА Покажи множество решений на числовомлуче. Выпиши множество решении нера-9венств...
1
1)
Введём замену: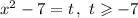 .
.
Уравнение становится вот таким:
Используем теорему Виета:
Получили два значения, которые управляют ОДЗ переменной t. Выполняем обратную замену:
Уравнение имеет 4 решения.
ответ: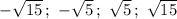 .
.
2)
Сразу установим, что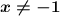 , поскольку тогда знаменатель обратится в 0.
, поскольку тогда знаменатель обратится в 0.
Вводим замену: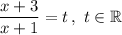 .
.
Уравнение принимает вид:
Теперь выполняем обратную замену:
Решим каждое уравнение отдельно. Начнём с верхнего:
И теперь решим нижнее:
ответ: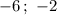 .
.