Решить уравнение, подробно
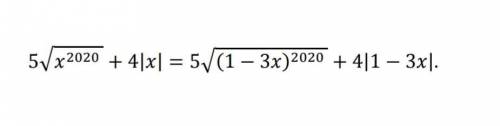
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) Обчисліть масу кальцій карбонату (CaCO3) кількістю речовини 2, 5 моль. 2) Яка...
2 - Начертите отрезок мк и отметьте на нем точку n такую, что mn:nk=5:2...
3 - Сложение одночленов сверху фото для решения...
2 - Реши задачу и запиши вывод: прямоугольник разделен на 3 части. Площадь первой части...
3 - Вычисли разность: 1 1\21 − 3\12 = (запиши несократимую дробь)....
1 - С какой стороны начинается обратное перестроение после перестроения из колонны...
2 - №4 тапсырма, Суретте таразынын, сол нак, таблитсия бял күй1 муас не500 г картасы,...
1 - «Національно-визвольна українського народу у 17 столитті була випадковою чи закономірним...
1 - Автор Эзоп Эзоп Бабрий С.Михалков Признаки жанра «Лисица и виноград» «Волы и ось»...
2 - Массовая доля оксида железа равна 70% определите молекулярную массу этого оксида...
3
x1=1/4
x2=1/2
Объяснение:
5*√(x^2020) +4*|x| = 5*√( (1-3x)^2020) + 4*|1-3x|
Рассмотрим функцию
f(t) = 5*√(t^2020) +4*|t|
Наше уравнение можно записать в виде :
f(x) = f(1-3x)
Очевидно, что при t >=0 функция f(t) монотонно возрастает при возрастании аргумента t .
Так же очевидно , что функция четная
f(-t) = 5*√((-t)^2020) +4*|-t| = 5*√(t^2020) +4*|t| = f(t) , то есть функция симметрична оси y , причем f(0)=0
Откуда очевидно , что если аргументы t1 и t2 не равны по модулю
|t1|≠|t2| , то и f(t1)≠f(t2) иначе это противоречило бы монотонному возрастанию функции на t>=0 или четности функции.
То есть f(t1) = f(t2) тогда и только тогда , когда аргументы t1 и t2 равны или противоположны .
Иначе говоря |t1|=|t2|
Таким образом из уравнения
f(x) = f(1-3x)
Следует уравнение
|x|=|1-3x|
1) x= 1-3x
4x=1
x1=1/4
2) -x= 1-3*x
2x=1
x2=1/2