Решить уравнение методом введения новой переменной x/x2-2+6 x2-2/x =7
Другие вопросы по теме Алгебра
Популярные вопросы
- Составте предложения по немецкому с переводом...
3 - УголBAC=125градусов нарисовать угол...
3 - До ть з тестом 1)Укажи кількість речовини 2086,2 г сахарози. Відповідь...
3 - Якою є місія Будди? Чи змінився Кандата у пеклі ? За що він був...
2 - Сделай Тебе не сложно а мне приятно)))...
3 - с химией завтра сдавать надо...
2 - Какие действия относятся к обработке графической информации в среде...
3 - Запиши слова в алфавитном порядке выбирая из скобок нужную букву...
1 - Решите это задание на тему: Атомна і ядерна фізика...
1 - А1 Укажите правильные утверждения: 1) атомы серы в степени окисления...
3
Сделаем замену:
Тогда:
Домножим на t:
Решим:
Делаем обратную замену:
1)
2)
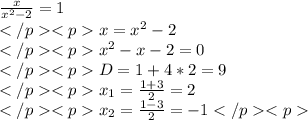
ответ:x=3/2; x=-4/3; x=2; x=-1.P. S.
В следующий раз пользуйтесь скобками и записывайте степень как ^
x/(x^2-2)+6*((x^2-2)/x)=7
Решить уравнение методом введения новой переменной
x/(x²-2)+6*(x²-2)/x = 7
ответ: { - 4/3 , - 1 , 3/2 , 2 } * * * { -1 1/3 ; - 1 ; 1,5 ; 2 } * * *
Объяснение: x/(x²-2)+6*(x²-2)/x =7
ОДЗ: { x≠0 ; x²-2≠ 0 . ⇔ x≠ { -√2 ; 0; √2 }
замена: t =x/(x²-2)
t + 6 /t =7 || t≠0 || ⇔t² -7t + 6=0 ⇒ t₁ =1 ,t₂= 6 ( По теореме Виета )
Обратная замена
а) x/(x²-2) =1 ⇔ x= x²-2 ⇔x²-x-2 =0 ⇒ x₁ = - 1 , x₂= 2 ;
б) x/(x²-2) =6 ⇔ 6x² - x - 12 =0 D = 1² -4*6*(-12)=289 =17²
x₃,₄ =(1 ±17) /( 2*6) x₃ =(1-17)/12 = - 4/3 , x₄ = 3/2.