решить уравнение логарифмы с ОДЗ
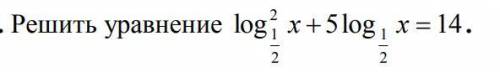
Другие вопросы по теме Алгебра
Популярные вопросы
- Знайдіть відсоток вмісту цукру в розчині, якщо в 400 г розчину міститься...
1 - Рассчитайте массовые доли %: кальция в его оксиде фосфора(iii) в его оксиде...
3 - На координатной прямой с еденичным отрезком 1 см дана точка а(-2). окружность...
2 - Кпд теплового двигателя всегда меньше 100% потому,что...
1 - Какая особенность размножения свойственна пресмыкающимся и птицам?...
1 - Чем вы объясните усиление внимания петра к развитию научных знаний? (развернутый...
1 - Почему видеокамера круглая а телевизор квадратный? ответ аргументировать...
1 - Определите эквивалентный объем кислорода участвующего в реакции s+o2=so2...
2 - Рассчитайте минимальный объём (н.у.) оксида углерода(4),который нужно пропустить...
2 - 3x-y=3 3x-2y=0 решите системой сложения...
2
Объяснение:
ОДЗ: x>0 x∈(0;+∞).
Пусть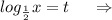
ответ: x₁=128 x₂=1/4.