Решить уравнение log1/9(2x^2-2x-1)=-1/2
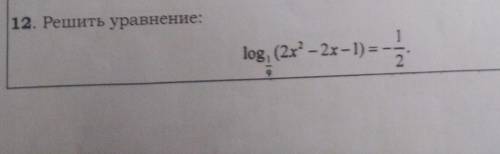
Другие вопросы по теме Алгебра
Популярные вопросы
- Сплошной однородный металлический шар радиуса R зарядили зарядом...
3 - Спортивна федерація зі спортивної гімнастики одержала статус...
3 - Нок и Нод чисел (6 и 8) (9 и 15) (28 и 21)...
1 - в равносторонний треугольник вписана окружность радиуса 5 см....
1 - Опишіть, користуючись картами атласу,річку Амазонку за планом:...
2 - Қоймада 912 ц көгөніс бар еді. Бірдей мөлшердегі 9 мәшинемен...
2 - Які художні засоби виділені в рядках: за сонцем змаронька ПЛИВЕ...
2 - решить, 5 или 6 задачу, если кто знает обе От...
1 - Складіть схеми трофічних ланцюгів із наведених організмів,,позначте...
3 - Знайди корені неповного квадратного рівняння 2x2−8=0. (Спочатку...
3
(см. объяснение)
Объяснение:
В решении уравнения покажем, что в нахождении ОДЗ нет необходимости.
Видим, что при любом найденном корне будет выполняться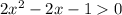 .
.
Тогда:
Значит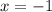 или
или 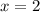 .
.
Уравнение решено!
-1;. 2
Объяснение: На фото