решить уравнение интегралов
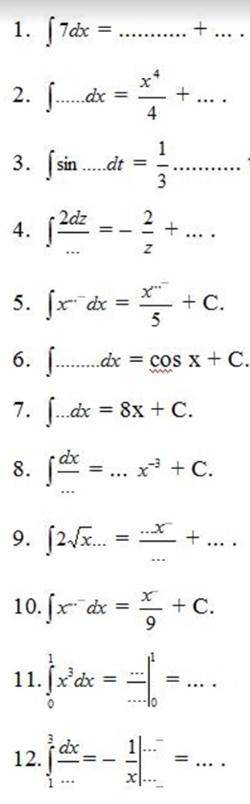
Другие вопросы по теме Алгебра
Популярные вопросы
- Скласти схему обставина присудок означення пiдмет...
3 - Продолжите фразу i would like 4-5 предложений, 34...
1 - Сюжетний ланцюжок твору камінний хрест в. стефаник...
2 - Девочка прошла от дома по направлению на запад 500 м. затем...
1 - Стороны треуголька относятся как 2: 3: 4 p треугольника = 137,7...
2 - Какие части речи следуют друг за другом в предложении «э, а я?...
2 - Биология вставьте в скобки слово, заканчивающее первое слово и...
3 - Найти область определения функции: 1. [tex]y = \sqrt[10]{4 - log_{2}(x)...
1 - Сделайте сочинение-рассуждение на тему растения четвёртый класс...
2 - Есть два типа емкостей , один из которых может вмещать 2 4/7 литров...
1
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.