Алгебра: Решить уравнение cos^2x-3sin^2x=-sin^2x

Решить уравнение cos^2x-3sin^2x=-sin^2x

Ответы

Даниил12345666 09.10.2020 22:25

Решить уравнение.

$cos^2(x) - 3sin^2(x) = -sin^2(x);\\cos^2(x) = 3sin^2(x) - sin^2(x);\\cos^2(x) = 2sin^2(x).$

Если sin²(x) = 0, то cos²(x) по данному уравнению тоже должен быть равен нулю. Но из основного тригонометрического тождества sin²(x) + cos²(x) = 1. Получено противоречие, ведь 0 + 0 ≠ 1. Отсюда sin²(x) ≠ 0, значит имеем право делить на него.

$cos^2(x) = 2sin^2(x);\;|:sin^2(x)\\ctg^2(x) = 2;\\\left[\begin{array}{c}ctg(x) = \sqrt2,&ctg(x) = -\sqrt2;\end{array} \Longleftrightarrow\left[\begin{array}{c}x = arcctg(\sqrt2) + \pi k,\; k\in Z,&x = arcctg(-\sqrt2) + \pi m,\; m\in Z;\end{array}\Longleftrightarrow$

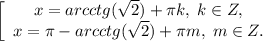
$\left[\begin{array}{c}x = arcctg(\sqrt2) + \pi k,\; k\in Z,&x = \pi - arcctg(\sqrt2) + \pi m,\; m\in Z.\end{array}$

ответ: $\bf x = arcctg(\sqrt2) + \pi k,\; k\in Z,\\x = \pi - arcctg(\sqrt2) + \pi m,\; m\in Z.$

ПОКАЗАТЬ ОТВЕТЫ

Tyshkanchik228 09.10.2020 22:25

$cos^2x-3sin^2x=-sin^2x\\\\cos^2x-3sin^2x+sin^2x=0\\\\(\underbrace {cos^2x+sin^2x}_{1})-3sin^2x=0\\\\1-3sin^2x=0\\\\3sin^2x=1\\\\sin^2x=\frac{1}{3}\\\\\frac{1-cos2x}{2}=\frac{1}{3}\\\\3\cdot (1-cos2x)=2\\\\3-3cos2x=2\\\\3cos2x=1\\\\cos2x=\frac{1}{3}\\\\2x=\pm arccos\frac{1}{3}+2\pi n\; ,\; n\in Z\\\\x=\pm \frac{1}{2}\cdot arccos\frac{1}{3}+\pi n\; ,\; n\in Z$