Решить уравнение. 9 класс, тема дробно-рациональные уравнения. Смотрела классную работу брата - очень запутанное решение, заменяли на t, потом через t искали x. Не смогла ему , стало интересно как же все таки это можно решить. С листка #8 и 9.

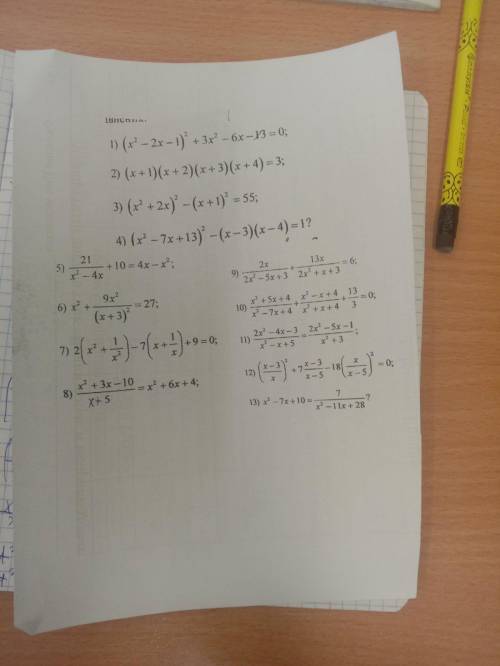
Решить уравнение. 9 класс, тема дробно-рациональные уравнения. Смотрела классную работу брата - очен

Ответы

Craftrik 22.01.2022 06:00

Ну, например, так:

8) Положим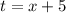 t = x+5 , тогда 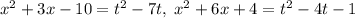$x^2+3x-10 = t^2-7t,\; x^2+6x+4 = t^2-4t-1$ , откуда уравнение принимает вид 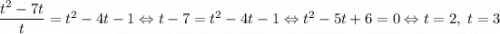$\dfrac{t^2-7t}{t} = t^2-4t-1 \Leftrightarrow t-7 = t^2-4t-1 \Leftrightarrow t^2-5t+6=0 \Leftrightarrow t=2,\; t=3$ , откуда $x=-3,\; x=-2$ .

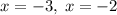9) Добавим к первой дроби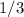 1/3 , получим 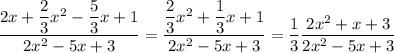$\dfrac{2x+\dfrac{2}{3}x^2-\dfrac{5}{3}x+1}{2x^2-5x+3} = \dfrac{\dfrac{2}{3}x^2+\dfrac{1}{3}x+1}{2x^2-5x+3} = \dfrac{1}{3}\dfrac{2x^2+x+3}{2x^2-5x+3}$ . А ко второй добавим 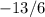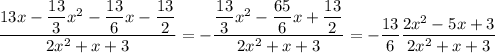-13/6 : $\dfrac{13x-\dfrac{13}{3}x^2-\dfrac{13}{6}x-\dfrac{13}{2}}{2x^2+x+3} = -\dfrac{\dfrac{13}{3}x^2-\dfrac{65}{6}x+\dfrac{13}{2}}{2x^2+x+3} = -\dfrac{13}{6}\dfrac{2x^2-5x+3}{2x^2+x+3}$ . Не забудем вычесть добавленные величины. После обозначения 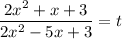$\dfrac{2x^2+x+3}{2x^2-5x+3} = t$ , получаем 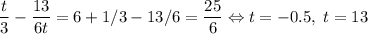$\dfrac{t}{3} - \dfrac{13}{6t} = 6+1/3-13/6=\dfrac{25}{6} \Leftrightarrow t=-0.5,\; t=13$ . Осталось решить два уравнения. 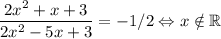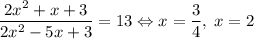Первое: $\dfrac{2x^2+x+3}{2x^2-5x+3} = -1/2 \Leftrightarrow x\notin \mathbb{R}$ , второе: $\dfrac{2x^2+x+3}{2x^2-5x+3} = 13 \Leftrightarrow x=\dfrac{3}{4},\; x=2$ .