Решить уравнение 2cos^2x - 5cosx =3

x₁ = 2π/3 + 2πn     (n ∈ Z)

x₂ = -2π/3 + 2πk     (k ∈ Z)

Объяснение:

2cos²x - 5 cosx = 3

2cos²x - 5 cosx -3 = 0

Замена t = cos x      t ∈ [-1; 1]

2t² - 5t - 3 = 0

D = 5² + 4 · 2 · 3 = 49 = 7²

t₁ = 0.25 · (5 + 7) = 3  не подходит, так как  t ∈ [-1; 1]

t₂ = 0.25 · (5 - 7) = -0.5

cos x = -0.5

x₁ = 2π/3 + 2πn     (n ∈ Z)

x₂ = -2π/3 + 2πk     (k ∈ Z)

Объяснение:

Пусть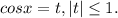   Тогда уравнение принимает вид:

Условию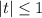 удовлетворяет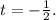

Значит