Решить уравнение 2) укажите корни этого уравнения, принадлежащие отрезку [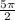 и
и 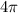 ]
] 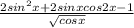
Другие вопросы по теме Алгебра
Популярные вопросы
- Последствия. 1. Опустошение страны 2. Экономическое и культурное отставание...
1 - КТО-НИБУДЬ Какое наибольшее число нулей может оказаться в бесконечной...
2 - Руский упр 74 6класс Зеленина...
2 - КК ПОДКАТИТЬ К ОДНАКЛАСТНИЦАМ ? в 6 классе...
2 - титул пер-о переводится как...
2 - 4,4 и я получил 2 какая оценка будеt...
3 - Твір на тему Правила харчування та чому важливий питний режим*Швидко...
2 - Денис разбил треугольник на девять треугольничков, как показано на рисунке,и...
2 - с решением Алгебра 10 класс «Числовые Функции»...
2 - Complete the sentences with the right purpose of a preposition by four...
3
Ниже↓
Объяснение:
Числитель 2sin²x+2sinx*cos2x-1=
=2sin²x+2sinx*(cos²x-sin²x)-(sin²x+cos²x)=
=sin²x- cos²x +2sinx*(cos²x-sin²x)=
=(sin²x- cos²x) -2sinx*(sin²x-cos²x)=
=(sin²x- cos²x)(1 -2sinx)= -( cos²x- sin²x)(1 -2sinx)=-cos2x(1 -2sinx). {-cos2x(1 -2sinx)=0
{cosx>0
Решим первое -cos2x(1 -2sinx)=0
1) cos2x=0, 2х=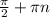 , х=
, х=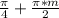 , m∈Z
, m∈Z
2) 1 -2sinx=0 , sinx=1\2 , х=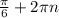 x=
x=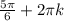 , n,к∈Z
, n,к∈Z
Решим второе
cosx>0 , х∈ (-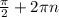 ;
; 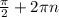 ). Выберем из найденных корней п 1, удовлетворяющие полученному условию. .
). Выберем из найденных корней п 1, удовлетворяющие полученному условию. .
Это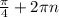 ,
, 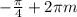 ,
, 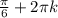 где n, m, k∈ Z
где n, m, k∈ Z
Выберем корни из [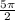 ;4π ]
;4π ]
Для х=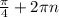 нет ,
нет ,
Для х=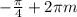 это
это 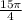 .
.
Для х=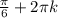 нет.
нет.
2sin²x+2sinxcos2x-1)/(√cosx)=(2sin²x+2sinxcos2x-1)/(√cosx)=
(2sinxcos2x-cos2x)/(√cosx)=cos2x(2sinx-1)/(√cosx)
ОДЗ : cosx>0;х∈(-π/2+2πm; π/2+2πm); m∈Z;
cos2x=0; х=π/4+πn/2; n∈Z;
sinx=1/2; х=(-1)ⁿπ/6+πк; n∈Z; его лучше расписать для четного и нечетного к. Если к четное , то к=2t; х=π/6+2πt ; t∈Z;
Если к нечетное , то к=2t + 1; х=5π/6+2πt ; t∈Z; этот ответ не подходит, т.к. не входит в ОДЗ.
Найдем корни уравнения из указанного отрезка.
а) х=π/4+πn/2; n∈Z;
2.5π≤π/4+πn/2≤4π; 2.5≤1/4+n/2≤4; 2.25≤n/2≤3.75; 4.5≤n/2≤7.5;
n=5; х=π/4+5π/2=∉ОДЗ,
n=6; х=π/4+6π/2=13π/4∉ОДЗ,
n=7; х=π/4+7π/2=15π/4
б) х=π/6+2πt ;
5/2≤1/6+2t≤4
5/2-1/6≤2t≤4-1/6
7/3≤2t≤23/6
7/6≤t≤23/12 нет здесь корней из указанного отрезка.