Решить уравнение (1/6)*log₂ (x-2)-1/3+(1/6)*log₂ (3x-5)=0
Другие вопросы по теме Алгебра
Популярные вопросы
- что открыли вам прочитанное в этом разделе произведение и с Тургенева...
3 - ответить письменно на вопросы. А.Чехов «Размазня». 4. Анализ рассказа....
1 - До ть написати твір Я учень ...
2 - Діалог про правила поведінки під час ожеледиці використовуючи дієприкметникові...
3 - 1) Put the verbs in brackets into the Present Simple, Present Continuous,...
2 - Найдите протяженность амазонской низменности с севера на юг по меридиану...
3 - Звукова хвиля, яка створена джерелом звуку, що коливається з періодом...
1 - задано масив з n елементів знайти кількість елементів масива що дорівнюють...
3 - Осина и сосна, в чём сходство, а в чём отличие ...
3 - Дифференциальные уравнения) может кто шарит, вся информация в приложенном...
2
Объяснение:
ОДЗ: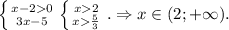
ответ: x=3.
Объяснение: (во вложении)