РЕШИТЬ ТРИГОНОМЕТРИЧЕСКОЕ УРАВНЕНИЕ!
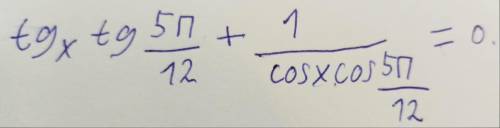
Другие вопросы по теме Алгебра
Популярные вопросы
- Официальная религия Монгольской империи в XIII в.: буддизм официальной религии...
1 - Округли числа 12 344; 12 348; 56835; 56831; 9981, 9999 до десятков. Задание 2...
2 - с историей! Всего один во б...
2 - Обчислити сторони ромба, якщо його площа 216 см2, а одна з діагоналей 24 см....
2 - решить задание по геометрии...
2 - Дано: АВСД- прямоугольник, ВД- диагональ. Угол АДВ равен 15 градусам, а угол...
3 - Тест «Вводные слова» Вариант 1 1. В каком варианте ответа правильно указаны все...
2 - Преобразование неправильных дробей Подберите каждой неправильной дроби равную...
1 - Кто знает как сделать такую штуку...
1 - Choose the correct item. 1. Would you like a jar/bottle of cola? 2. Low-fat yoghurt/lamb...
2
Объяснение:
Домножим на знаменатель, избавившись, при условии, если:
k ∈ Z