решить тригонометрические уравнения! 1) cosx+1/2=0
2) 2sinx=√3
3) sin3x=-1
4) tgx+2=0
5) (ctgx+1)(tgx-1)=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Оберіть твердження, які характеризують діяльність гетьмана К. Розумовського:1)...
2 - Тәуелсіздік тау етер жалгыз кие эссе...
3 - ,ДАЮ 100 б. В. Почему А.П. Чехов назвал свой рассказ «Попрыгунья»? Дмитрия...
2 - Чим менше вразила казка про маленького принца опис...
2 - Розв яжіть рівняння: 12,48 : (х – 1,564) -0,6 =9,4...
1 - Найти высоту паралипепеда, если объем V-48³...
3 - твір-роздум в худ.стилі Характеристика Івана сили...
2 - 8. I turned the TV and watched a cartoon. a. to b. for c. on...
3 - Бисдро 7 клас алгебра 1 варіант...
3 - Задание 1. Выберите один ответ из нескольких предложенных. 1. Лизавета...
1
1)
x1 =2 /3+2k
/3+2k
x2 =4 /3+2k
/3+2k
2)
x1 = /3+2k
/3+2k
x2 =2 /3+2k
/3+2k
3)
x1 = /2+2k
/2+2k /3
/3
4)
x = -arcos(2) + k
5)
x = /4+k
/4+k /2
/2
Объяснение:
1) cos(x)+1/2 =0
cos(x) = -1/2
x1 =2 /3+2k
/3+2k
x2 =4 /3+2k
/3+2k
2) 2sin(x)=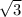
sin(x) =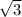 /2
/2
x1 = /3+2k
/3+2k
x2 =2 /3+2k
/3+2k
3) sin3x=-1
x1 = /2+2k
/2+2k /3
/3
4) tgx+2=0
tgx = -2
x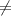
 /2+k
/2+k
x = -arcos(2) + k
5) (ctgx+1)(tgx-1)=0
(ctgx+1)(tgx-1) = -2/tan(2x)
x = /4+k
/4+k /2
/2