Решить тригонометрические уравнение. sin^12x+cos^5x=1 (синус в двенадцатой степени икс плюс косинус в пятой степени икс равно единице)

так как для любого действительного х: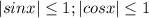

то

поэтому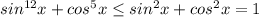

причем равенство достигается только тогда когда

 а

 а

откуда из первого sin x=1 V sin x=-1 V sin x=0

со второго cos x=1 или cos x=0

учитывая, что когда sin x=1 V sin x=-1 то cos x=0 (по основному тригонометрическому тождеству) а когда cos x=1 то sin x=0, по модулю одновременно они не могут быть равными 1, то

решениями будут

ответ: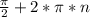 n є Z 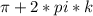; k є Z