Решить тригонометрческие уравнения на фото
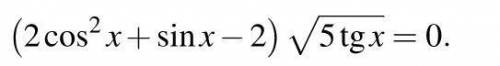
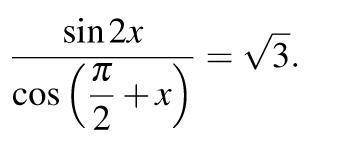
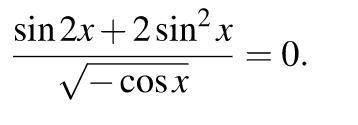
Другие вопросы по теме Алгебра
Популярные вопросы
- При каких значениях параметра a график функции f(x)=(a+1)x^2-4x+2...
2 - Знайди значення виразу 9,1-(8,169+7,311): 2. решить...
1 - Обчисліть роботу, яка здійсниться при проходженні через спіраль...
1 - Оброзуй однокоренные слова сущ-ное,глагол,прилагательное : соль,...
1 - Молекулярную кристаллическую решётку имеет каждое из двух веществ:...
3 - Из данного предложения выпишите одно подчинительное словосочетание...
2 - Производная функции y=✓x^3+x^2+3x-15...
3 - С! четверть пути автомобиль двигался со скоростью 120 км/ч, а остаток...
3 - Решить : тонкостенный цилиндрический сосуд с площадью горизонтального...
2 - Ясама стараюсь у огня по частям снежинку разобрать. , сделать синтаксический...
3
1.
Ограниченте на тангенс:
Тангенс неотрицателен когда его аргумент лежит в 1 и 3 четвертях, значит и корни исходного уравнения дрожи сдесь лежать:
2.
ОДЗ: