решить тригометрическое уравнение. В конце решения захожу в тупик. cosx= корень3/2 хє[-2п;п]
Другие вопросы по теме Алгебра
Популярные вопросы
- Катер плыл по течению реки 3 ч и против 4 ч.какое расстояние катер за...
3 - Решить уравнение ( 2,61 - 4х) / 0,03+4,6=90...
2 - Fill in the correst prepositions astana is the capital kazakhstan. 2.i...
3 - Мне нужен рассказ на презентацию о великой екатерине ii !...
2 - Произведение чисел 67и80 уменшить в 5 раз и полученное частное увеличьте...
1 - Правители галицко-волынского княжества...
1 - Три четвертых плюс семь двадцать пятых...
3 - Скласти речення з словами тато .знання, пісня, підсніжник...
2 - Втрубе переменного сечения в сечении площадью 20 см2 скорость течения...
3 - Прочитай текст. в каком времени и числе стоят глаголы? как изменится...
3
Отбор корней:
Делим на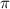
Получим два неравенства:
и
Первое неравенство верно при n=0
Второе неравенство верно при n=-1;0
Получили три корня: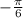 ;
; 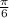 ;
; 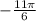
принадлежат отрезку [-2π;π]
Объяснение:
cosx=√3/2
х=±arccos√3/2+2πn; n∈Z
х=±π/6+2πn; n∈Z
х=π/6+2πn; n∈Z
-2π≤π/6+2πn≤π
-2≤1/6+2n≤1
-1 1/12≤n≤5/12
n=-1; х=13π/6
n=0; х=π/6
х=-π/6+2πn; n∈Z
-2π≤-π/6+2πn≤π
-1≤-1/12+n≤1/2
-11/12≤n≤7/2
n=0; х=-π/6