Решить) своими силами не получается!

а) Эллипс .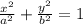

Подставляем координаты точек А и В.

(0²/a²) + ((√3)²/b²) = 1. Отсюда b = +-√3.

((√(14/3)²/a²) + (1²/b²) = 1 подставим b = +-√3.

((14/3)/a²) + (1/3) = 1,

((14/3)/a²) = 2/3,

3a² = 21,

а = +-√7.  

ответ: уравнение эллипса (x²/(√7)²) + (y²/(√3)²) = 1.

б) Гипербола.

Так как в задании в уравнениях асимптот b = 0, то центр гиперболы в начале координат.

Уравнение асимптот: у = +-(b/a)x = √21/10.

Так как b/а = √21/10 дано в задании, то сразу имеем значения полуосей: а = 10, b = √21 и получаем уравнение гиперболы:

(x²/(10²) - (y²/(√21)²) = 1.

Проверим значения а и b по заданному эксцентриситету: b²/a² = ε² - 1.

Получаем: 21/100 = 121/100 - 1 = 21/100.

Значит, уравнение верно составлено.

в) Парабола.

Уравнение директрисы для параболы, у которой  фокальная ось совпадает с осью Oy, имеет вид у = -р/2, а  уравнение параболы имеет вид: x²=2py.

Директриса: у = -4 = -р/2, отсюда р = 8.

Получаем уравнение параболы:  x²=2*8y.