1. Алгебра
  2. Решить СЛАУ методом

Решить СЛАУ методом Гаусса


Решить СЛАУ методом Гаусса

roky210 roky210    1   03.12.2021 18:27    1

Ответы
serofimtimoxa serofimtimoxa  18.01.2022 09:19

метод Гаусса

Объяснение:


Решить СЛАУ методом Гаусса
ПОКАЗАТЬ ОТВЕТЫ
Босс05 Босс05  18.01.2022 09:19

\begin{equation*}\begin{cases}x_1 + x_2 + 5x_3 = -7\\2x_1 + x_2 + x_3 = 2\\x_1 + 3x_2 + x_3 = 5\end{cases}\end{equation*}

\begin{pmatrix} 1& 1&5\Big|&-7\\ 2& 1&1\Big|&2\\ 1&3&1\Big|&5\end{pmatrix}

Первую строку оставляем без изменений. Вторую складываем с первой, умноженной на -2, результаты записываем во вторую. Из третьей строки вычитаем первую, результаты записываем в третью.

\begin{pmatrix} 1& 1&5\ \ \,\Big|&-7\\ 0& -1&-9\Big|&16\\ 0&2&-4\Big|&12\end{pmatrix}

Первую и вторую строки оставляем без изменений. Третью складываем со второй, умноженной на 2, результаты записываем во вторую.

\begin{pmatrix} 1& 1&5\ \ \,\,\,\Big|&-7\\ 0& -1&-9\,\,\,\Big|&16\\ 0&0&-22\Big|&44\end{pmatrix}

Переписываем третью строку в аналитическом виде.

-22x_3= 44\\\\\boxed{\boldsymbol{x_3 = -2}}

Значение одной переменной нашли. Переходим к следующей. Переписываем вторую строку в аналитическом виде.

-x_2-9x_3 = 16\\\\x_2 = -16-9x_3 = -16-9\cdot(-2) = -16 + 18 = 2\\\\\boxed{\boldsymbol{x_2 = 2}}

То же самое делаем с первой строкой.

x_1 + x_2 + 5x_3 = -7\\\\x_1 = -7 - x_2 - 5x_3 = -7-2 - 5\cdot(-2) = -7-2 + 10 = 1\\\\\boxed{\boldsymbol{x_1 = 1}}

Нашли значения всех трёх переменных.

ответ: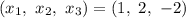 \left(x_1,\ x_2,\ x_3\right) = \left(1,\ 2,\ -2\right) .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
KseshaMail KseshaMail  10.03.2019 05:30
При смешивании 40%-ного раствора кислоты с 10%-ным раствором кислоты получили 800 г 21,25%-ного раствора. сколько граммов каждого раствора было для этого взято?...
Карташова111 Карташова111  10.03.2019 05:30
Сколько часов в 2 часах 40 минутах?...
зайка191111 зайка191111  10.03.2019 05:30
Вправильной треугольной пирамиде sabc p- середина ребра ab, s - вершина. известно, что вс = 5, а sp = 6. найдите площадь боковой поверхности пирамиды...
svetagres svetagres  10.03.2019 05:30
Найти количество целых решений неравенства |x-3|...
lolowkaujw lolowkaujw  10.03.2019 05:30
Знайти множину значень функції y= +2x...
mishtal2017 mishtal2017  10.03.2019 05:30
С. тема вычисление производной найдите производную функции: 1.y=-x^3 + 0,5x^2 - x +1 2.y= - 3cos x *(x^2 +2) 3.y=1/корень из x 4. y=1/sin x 5. y=x^4/3-x 6.y=x^2 + ctg...
ВРотКомпот ВРотКомпот  10.03.2019 05:30
Найдите производную функции: y=sin2xcosx-cos2xsinx сначала ведь надо разложить sin2x, а затем по формулам дифференцирования?...
vikailen vikailen  10.03.2019 05:30
F(x)= 3x-√x+13 при каких значениях х выполняется равенство f(x)=1...
rudneva04 rudneva04  10.03.2019 05:30
Найдите все такие двузначные натуральные числа, при перестановке цифр в которых это число: увеличивается на 75%....
norley15 norley15  10.03.2019 05:30
Найдите наименьшее целое число ,входящее в область определения допустимых значений х+7,6 (всё под корнем) 2.найдите сумму абсцисс точек пересечения графиков функции у=7х-8...

Популярные вопросы