Решить системы логарифмических уравнений и неравенств

Другие вопросы по теме Алгебра
Популярные вопросы
- Выпишите из предложения сочинительный союз и укажите его вид. 1. Надя возмущалась...
2 - Вычесли расстояние велосебедиста если его скорость 13 км/ч...
1 - Определите последовательность процесса образования семени в результате двойного...
3 - Проведите по общей схеме исследование функции и постройте ее график у = – х2...
3 - 25% его равны 45 20% его равны 2 50% его равны 7 1% его равны 6 8% его равны...
1 - Найдите точку максимума функций: P.s. Распишите решение...
3 - Определите массу этилового спирта полученного при спиртовом брожении 720 граммов...
1 - Найдите площадь многоугольника, изображенного на клеточной бумаге с размером...
1 - К 11% от числа700 прибавьте 2% от числа 980....
2 - Выполните синтаксический разбор предложения : Постепенно жывие существа заселили...
2
ответ: A)
Б)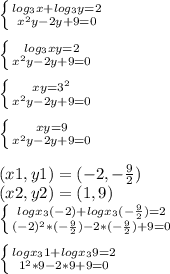
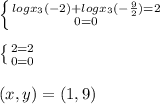
2.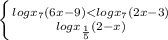 ≥
≥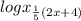
Решаем систему неравенств
Находи пересечение x ∈ [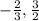 〉 , x ∈ 〈
〉 , x ∈ 〈 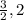 〉
〉
x ∈ ∅