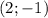решить систему уравнений x(1+y)+4=-4Y x^2+y^2=5
Другие вопросы по теме Алгебра
Популярные вопросы
- Поясніть сенс назви оповідання: Подорожній, коли ти прийдеш у Спа......
2 - Рассчитать энергию светового кванта зелёного света с длиной волны...
3 - Найди производные функции y=x^2-5x+9...
1 - ∫√(lnx )⋅dx/x Найти неопределенный интеграл...
3 - Напечатать решение заданного задания THEMA: Die zusammengesetzten...
2 - Опираясь на статьи Судебника 1550 года, докажите, что в России...
1 - решить примеры решить примеры...
3 - Творчество М.Е.Салтыкова-Щедрина. Жизненный и творческий путь....
1 - Кто заполняет нормативные и законодательные акты регулирующие договорные...
1 - Pliz решите за меня новая тема а на карантине разбираться нужно...
2
О т в е т.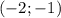 ;
;