1. Алгебра
  2. Решить систему уравнений

Решить систему уравнений первое уравнение. квадратный корень (х² - у²) + квадратный корень (х - у) =4 второе уравнение. 1/ квадратный корень (х - у) - 1/ квадратный корень (х² - у²) =1/3

Шенявка Шенявка    3   14.06.2019 18:50    5

Ответы
Jdjsjsbbsbsbдевочка Jdjsjsbbsbsbдевочка  02.10.2020 02:08
\sqrt{x^2-y^2}+\sqrt{x-y}=4\\\\\frac{1}{\sqrt{x-y}}-\frac{1}{\sqrt{x^2-y^2}}=\frac{1}{3} 

            \sqrt{(x-y)(x+y)}+\sqrt{x-y}=4,\; \; \; \; \; u=\sqrt{x-y},\; v=\sqrt{x+y}\\\\\frac{1}{\sqrt{x-y}}-\frac{1}{\sqrt{(x-y)(x+y)}}=\frac{1}{3}\\\\ \left \{ {{u\cdot v+u=4} \atop {\frac{1}{u}-\frac{1}{u\cdot v}=\frac{1}{3}} \right. \; \left \{ {{u(v+1)=4} \atop {\frac{u(v-1)}{u\cdot v}}=\frac{1}{3}} \right. \; \left \{ {{u=\frac{4}{v+1}} \atop {\frac{(v-1)}{v}=\frac{1}{3}}} \right. \; \left \{ {{u=\frac{4}{v+1}} \atop {3(v-1)=v}} \right. \; \left \{ {{u=\frac{8}{5}} \atop {v=\frac{3}{2}}} \right.

\sqrt{x-y}=\frac{8}{5}\; \; \to \; \; x-y=\frac{64}{25}\\\\\sqrt{x+y}=\frac{3}{2}\; \; \to \; \; x+y=\frac{9}{4}\\\\2x=\frac{481}{100},\; \; x=2,405\\\\2y=-\frac{31}{100},\; \; y=-0,155
ПОКАЗАТЬ ОТВЕТЫ
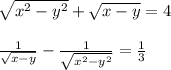
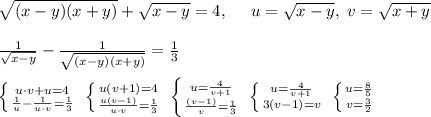
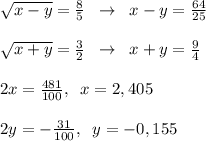
Другие вопросы по теме Алгебра
SiperV2 SiperV2  12.05.2020 19:15
У выражение sin(π-a) *cos(π/2+a)/cos(-a) *sin(-a)...
nzinulla nzinulla  12.05.2020 19:15
Зоране У выражение 3ху –3х – ( х−3 ху)...
DarinaLove11 DarinaLove11  12.05.2020 19:14
A) 5a²b; 3\5ab³і 3ac⁴ б)-8xy; (-2,5)b² i 0,1ax​...
yoongiswag yoongiswag  12.05.2020 19:14
Яке з поданих рівнянь має два різні корені? 1) х² - 2х + 4 = 0 2)3х² + 4х - 8 = 0 3)25х² - 10х + 1 = 0 4)2х² + 5х + 4 = 0...
RedHamster RedHamster  12.05.2020 19:14
Найди значение выражения наиболее рациональным это дроби)...
SoftMGDN SoftMGDN  12.05.2020 19:13
Нужно построить график, табличкаy=|x|, y=5x-3​...
адильчичек адильчичек  29.10.2019 02:57
Вычислить: корень 7, 5x корень 0, 3 ; ​...
krut2202 krut2202  29.10.2019 02:41
Корень 7,5 x корень 0, 3вычислить​...
Sergovseznaet Sergovseznaet  29.10.2019 05:15
Решите 1 и последнее (4 не надо). надо...
МастерФейк МастерФейк  29.10.2019 05:14
2. взять производные функций: а) у = 3x ln ( 4х – х? ) б) y = arctg 2х10 3. решить однородное линейное дифференциальное уравнение второго порядка 9y — бу – 24y = 0 найти частное...

Популярные вопросы