Решить систему уравнений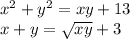
это одна система
​

x² + y² = xy + 13

x + y = √xy + 3

x, y одного знака > 0

(x + y)² = x² + y² + 2xy

x² + y² = (x + y)² - 2xy

замена

√xy = t > 0

x + y = u

Система

u² = 3t² + 13

u = t + 3

t² + 6t + 9 = 3t² + 13

2t² - 6t + 4 = 0

t² - 3t + 2 = 0

D = 9 - 8 = 1

t12 = (3 +- 1)/2 = 1   2

1. t = 1

u = 4

√xy = 1

x + y = 4

x = 4 - y

y(4 - y) = 1

y² - 4y + 1 = 0

D = 16 - 4 = 12

y12 = (4 +- √12)/2 = 2 +- √3

y1 = 2 + √3

x1 = 4 - y1 = 2 - √3

y2 = 2 - √3

x2 = 2 + √3

2. t = 2

u = 5

√xy = 2

x + y = 5

x = 5 - y

y(5 - y) = 4

y² - 5y + 4 = 0

D = (25 - 16) = 9

y34 = (5 +- 3)/2 = 1  4

y3 = 1

x3 = 5 - y3 = 4

y4 = 4

x4 = 1

ответ (1, 4) (4, 1) (2 - √3, 2 + √3) (2 + √3, 2 - √3)