Решить систему линейных уравнений по методу Гаусса
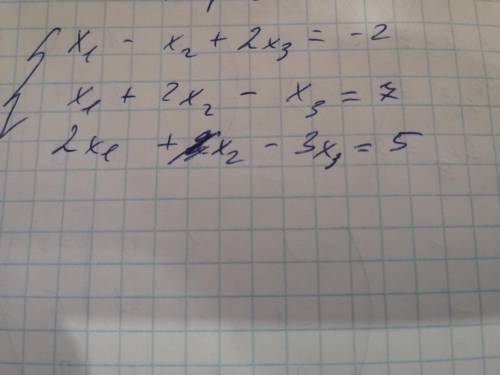
Другие вопросы по теме Алгебра
Популярные вопросы
- 40 ! проанализируйте любую главу из повести м. горького «детство»,...
1 - На рисунке прямые a и b параллельны,угол 1 равен 28 найдите угол...
2 - Доведіть що при будь-ікому натуральному n значення виразу 3^n+2...
3 - Поведение аси из повести тургенева“ася”и с чем это связано в каждой...
2 - Дополните предложения используя правильную форму прилагательных...
2 - Используя оператор цикла, составить алгоритм ( словами : целое,...
1 - Сцифр 9 1 7 составьте все двузначные числа...
2 - Составить текст на любую тему с nothing never nowherе nobody...
1 - 1. укажите правителя, который ввёл государственную оплату билета...
3 - Сделать характеристику ромео и характеристику джульетти из повести...
3
Объяснение:
x1 - x2 + 2x3 = -2
x1 + 2x2 - x3 = 7
2x1 + x2 - 3x3 = 5
Перепишем систему уравнений в матричном виде и решим его методом Гаусса
1 -1 2 -2
1 2 -1 7
2 1 -3 5
от 2 строки отнимаем 1 строку, умноженную на 1; от 3 строки отнимаем 1 строку, умноженную на 2
1 -1 2 -2
0 3 -3 9
0 3 -7 9
2-ую строку делим на 3
1 -1 2 -2
0 1 -1 3
0 3 -7 9
к 1 строке добавляем 2 строку, умноженную на 1; от 3 строки отнимаем 2 строку, умноженную на 3
1 0 1 1
0 1 -1 3
0 0 -4 0
3-ую строку делим на -4
1 0 1 1
0 1 -1 3
0 0 1 0
от 1 строки отнимаем 3 строку, умноженную на 1; к 2 строке добавляем 3 строку, умноженную на 1
1 0 0 1
0 1 0 3
0 0 1 0
x1 = 1
x2 = 3
x3 = 0
Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:
1 - 3 + 2·0 = 1 - 3 + 0 = -2
1 + 2·3 - 0 = 1 + 6 + 0 = 7
2·1 + 3 - 3·0 = 2 + 3 + 0 = 5
Проверка выполнена успешно.
x1 = 1
x2 = 3
x3 = 0
ЕСЛИ НЕ ПОНЯТНО, ТО ВОТ ССЫЛКА:https://ru.onlinemschool.com/math/assistance/equation/gaus/