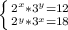 Решить систему через дискриминант
Решить систему через дискриминант
Другие вопросы по теме Алгебра
Популярные вопросы
- Марине нужно прочитать книгу,в которой 250 страниц. утром она...
3 - Для дачи купили 12 одинаковых стульев на сумму 2268 р.и 2 стола.стул...
3 - Какое транспортное средство следует обходить спереди...
1 - Автомобиль за 5 ч должен прибыть в указанный пункт ,не поменяя...
1 - Найдите ошибки в этом тексте и назовите их. трудный этот язык,...
1 - Горизонтальная платформа массой m1=120 кг вращается о чаcтотой...
2 - Таблица по характеристика климатических поясов климатический пояс...
3 - Вчем проявилось преимущество построения римского войска в решающем...
3 - Проверочные слова к словам: к_саться ; м_хать ; св_ркать ; т_лкать...
1 - Семья афониных состоит из шести человек. бабушке 65 лет, она пенсионерка....
2
2^x * 3^y = 12
2^y * 3^x = 18
2^x * 3^y = 2^2*3
2^y * 3^x = 2 * 3^2
x = 2 y = 1
или делим первое на второе
2^x * 3^y / 2^y * 3^x = 12 / 18
(2/3)^x*(3/2)^y = 2/3
(2/3)^(x-y) = 2/3
x - y = 1
умножаем первое на второе
2^x * 3^y *2^y * 3^x = 12 * 18
2^(x + y)*3^(x + y) = 6^3
6^(x + y) = 6^3
x + y = 3
x = 2
y = 1