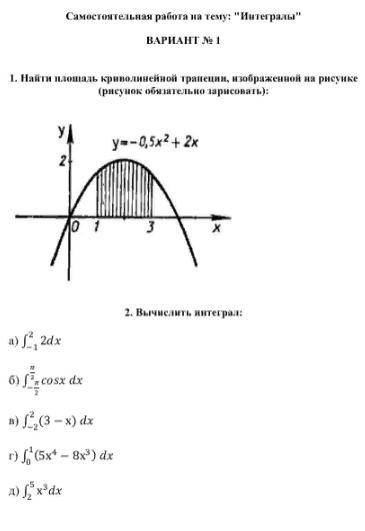
решить самостоятельную работу по математике
Другие вопросы по теме Алгебра
Популярные вопросы
- Слово подстилка,как проверить букву д в приставке...
2 - Скиньте скрин стиха анны ахматовой победа! нужно...
2 - Read and match the word in bold to the pictures перевод...
2 - Впод давление 2*10^5 па водяной пар от 150°с до 100°с. постройне график зависимости...
2 - Поезд первые 5 часов ехал со скоростью 72,8 км / ч и 4 часа со скоростью...
2 - Разместите на ленте времена имена: г.х андерсен, с. лагерлёф, м.м. пришвин...
1 - Постройки прямоугольник периметр который равен 17см...
2 - Суффиксальный образования слова...
2 - Вычисли по образцу 24+47-3 x9=24+47-27=71-27=44 это образец а вот само .1)35-27+3-0=...
3 - Предложение с предлогом a) всю дорогу они шли впереди. b) люблю сидеть около...
3
1)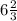
а) 6
б) 2
в) 5,5
г) -1
д) 152,25
Объяснение:
1 )
а)
б)
в)
г)
д)