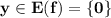решить примеры с доходчивым объянением. 1)
2)
3)
Как найти область значений функции? Чем отличается от области определения?
Другие вопросы по теме Алгебра
Популярные вопросы
- Каа я научился понимать язык цветов...
3 - Қар күреген бала сюжеттік желісі...
2 - Задание 3. 1. Придумайте и запишите рекламное объявление о выставке...
1 - Дописать уравнения ;MgO+H2O →MgO+HNO3 →MgO+SiO2→...
1 - С.Мұратюековтың Жусан иісі повесінен берілген үзіндіден Аянның...
2 - Заполните таблицу трассировки алгоритма согласно данной блок-схемы....
1 - Размеры параллелепипеда 126 см, 54 см и 28 см. Вычислите объем...
3 - A4+a10=16 і a2*a6=-12 Швидше !!...
2 - 1. На аснове якіх прымет можна сцвярджаць, што слова прачытаны...
2 - Два поезда идут навстречу друг другу. Один два пятых всего пути...
2
Відповідь:
Пояснення:
хЄ D( f ) ; y = f( x )Є E( f ) : D - обл. визначення ;
Е - множина значень функції .
1) f( x ) = 5 - x² ; E( f ) = (- ∞ ; 5 ] ;
2) f( x ) = | x + 2 | + 2 ; E( f ) = [ 2 ; + ∞ ) ;
3) f( x ) = √(- x² ) ; E( f ) = { 0 } .
Решение.
Это квадратичная функция , ограничений на переменную х не накладываются , поэтому
Графиком квадратичной функции является парабола, причём, т.к. коэффициент перед х² равен -1<0 , то ветви параболы направлены вниз , и выше вершины в точке (0;5) графика существовать не будет . Поэтому самое максимальное значение , которое принимает заданная функция равно f(x)=5 . Поэтому область значений функции
Cмотри рисунок .
Графиком этой функции является график функции у=|x| ( угол , ветви вверх ) сдвинутый вдоль оси ОХ на 2 единицы влево и вдоль оси ОУ на 2 единицы вверх .
ООФ: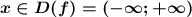
ОЗФ: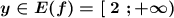
Смотри рисунок .
Под знаком квадратного корня может быть записано только неотрицательное выражение.
ООФ: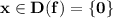 - это множество из одного элемента .
- это множество из одного элемента .
ОЗФ: