Решить пример sin(x/4)=sin^2(x/16)-cos^2(x/16)
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите глагол сослагательного (условного) наклонения: A ) занималась B ) тренировался...
3 - Изучите и решите по алгоритму в общем...
1 - с самостоятельной(с дано, СИ при необходимости и решением)...
1 - Яка маса автомобіля якщо рухаючись із швидкістю 54 км/Год під дією сили тертя 8000Н,...
1 - Какие черты характера Пугачева отмечает поэт?(Уникумы которые меня С в ОТВЕТЕ я...
2 - Укажите количество грамматических основ (рядом с номером предложения запишите цифру,...
1 - Сочинение по картине Енина Весна ...
3 - Морфологический разбор 2 любых глаголов из стиха А.Твардовского Рассказ танкиста...
1 - Кто в Османской империи носил титул Халифа? А) глава правительства Б) правитель...
2 - А Почему Раскольников чувствует себя приговоренного к смерти...
3
В левой части уравнения видим, что это формула косинуса двойного угла
Представим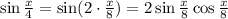 - синус двойного угла, получим
- синус двойного угла, получим
Произведение равно нулю, если хотя бы один из множителей равен нулю