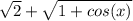решить пределы не применяя правила Лопиталя. Немного не понятно как это делать
Другие вопросы по теме Алгебра
Популярные вопросы
- Перечислите 10 штатов америки? : 3...
3 - Подобрать однокоренные слова: рожь,осень,нога,дорога,гнездо,вода,путь,гость,враг,долг,обещание...
2 - Найдите значение выражения х(х-у)-у(у^2-х при х=4 и у=2...
3 - Решите ! 1.найдите 4/9 от 23 022 4.найдите число,2/3 которого составляют...
3 - На столе в стопке 4 учебника.учебники и азербайджанский язык лежат на учебнике...
2 - Построить график y=-0.5x+2 с таблицей...
3 - Как вёл себя митраша оставшись один из повести кладовая солнца...
1 - Write only one word or one number in the answer box. emma is willy’s niece,...
2 - Между какими двумя последовательными членами арифметической прогрессии...
3 - Дано уравнение log2(x^2-4x+1)=3 (2 это основание логарифма) . вычислите...
1
2.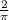
5.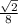
Объяснение:
2. Выполняем замену y=1-x => x=1-y
3. В условии, скорее всего ошибка. Должно быть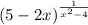
5. Умножаем числитель и знаменатель на