Решить показательные уравнения
 ( в ответе записать корень или произведение корней, если их несколько)
( в ответе записать корень или произведение корней, если их несколько)
 (найти количество отрицательных корней уравнения)
(найти количество отрицательных корней уравнения)
Другие вопросы по теме Алгебра
Популярные вопросы
- Акпарат туймедак ии как принимается...
1 - Составить и записать 2 предложения, употребив в них глаголы с приставками?...
3 - Как устанавливать шахматы на доске?...
2 - Выпиши из предложения подлежащее. укажи, какой частью речи оно выражено. пример:...
1 - :за первую неделю бригада рабочих заасфальтировала 2/7 дороги и еще 6 км после...
3 - Аквариум имеет форму прямоугольного параллепипеда с измерениями 25 см, 50 см...
1 - Найдите х,напишите однообразно им,либо правильную дробь либо неправильную дробь....
1 - Запиши число,которое содержит: 54 ед.второго класса и 863 ед. первого класса...
1 - 22-7-15 умножить на 4 умножить насемь поставить порядок действий...
1 - Постройте график функции y=2x-5 только чертежом...
2
3*4^x - 3^(x + 1/2) = 2^2x
(a^m)^n = a^mn
a^0 = 1 (a≠0)
3*4^x - 3^(x + 1/2) = 4^x
2*4^x = 3^(x + 1/2)
2 = 4^1/2
4^(x + 1/2) = 3^(x + 1/2)
(3/4)^(x + 1/2) = 1
x + 1/2 = 0
x = -1/2
26*5^(√(x^2 - √5*x)) = 25^(√(x^2 - √5*x) + 1/2) + 5
26*5^(√(x^2 - √5*x)) = 5^2(√(x^2 - √5*x) + 1/2) + 5
26*5^(√(x^2 - √5*x)) = 5*5^2(√(x^2 - √5*x)) + 5
5^(√(x^2 - √5*x)) = t > 0
26t = 5t² + 5
5t² - 26t + 5 = 0
D = 26^2 - 4*5*5 = 676 - 100 = 576 = 24^2
t12 = (26 +- 24)/10 = 5 1/5
1. t1 = 5
5^(√(x^2 - √5*x)) = 5
√(x^2 - √5*x) = 1
x^2 - √5*x = 1
x^2 - √5*x - 1 = 0
D = √5² + 4 = 9
x12 = (√5 +- 3)/2
x1 = (√5 + 3)/2 > 0
x2 = (√5 - 3)/2 < 0 (√5 < 3) да корень по условию
2. t1 = 1/5
5^(√(x^2 - √5*x)) = 1/5
√(x^2 - √5*x) = -1
корень четной степени на поле действительных чисел не может быть меньше 0
решений действительных нет
ответ один корень (√5 - 3)/2
1)
Возьмём логарифм по основанию 3/4 от обеих частей.
2)
Заменим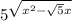 на t.
на t.
а)
Решений нет.
б)
Решив квадратное уравнение, получаем:
Так как √5 < 3, то один из корней меньше нуля.
ответ: 1.