Алгебра: Решить показательные уравнения и неравенства

Решить показательные уравнения и неравенства

Ответы

norley15 11.10.2020 17:44

$2. 1)1+3^{\frac{x}{2}}=2^x \\\\$

Докажем, что уравнение имеет не более 1 корня. Для этого слагаемое в правой части перенесем в левую часть со знаком минус, 1 - вправо, аналогично со знаком минус: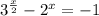 $3^{\frac{x}{2}}-2^x=-1$

Функция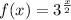 $f(x)=3^{\frac{x}{2}}$ монотонна возрастающая, а функция 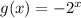g(x)=-2^x - монотонно убывающая для любого значения . Так как сумма монотонно возрастающей и монотонно убывающей функций есть функция монотонно возрастающая, а в правой части - функция постоянная, то графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Делаем вывод: исходное уравнение имеет не более 1 корня, что и требовалось доказать.

Методом подбора легко находим корень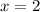 x=2 . Действительно: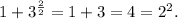 $1+3^\frac{2}{2}=1+3=4=2^2.$

ОТВЕТ: {2}

$2) (\frac{1}{2})^x+(\frac{\sqrt3}{2})^x=1$

Поступаем аналогично. В левой части - сумма двух монотонно убывающих функций, а значит функция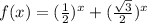 $f(x)=(\frac{1}{2})^x+(\frac{\sqrt3}{2})^x$ - монотонно убывающая. Справа имеем постоянную функцию. Следовательно, графики функций в левой и правой частях равенства имеют не более 1 точки пересечения. Т.е. исходное уравнение имеет не более 1 корня.

Методом подбора находим все тот же корень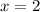 x=2 . Действительно: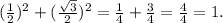 $(\frac{1}{2} )^2+(\frac{\sqrt3}{2})^2=\frac{1}{4}+\frac{3}{4}=\frac{4}{4}=1.$

ОТВЕТ: {2}

$3. |x-3|^{2x^2-7x}-10$

ОДЗ: |x-3| ≠ 1 ⇒ x ≠ 2; 4.

С учетом ОДЗ неравенство равносильно следующему:

(|x-3|-1)(2x^2-7x)0 ,

(|x-3|-1)(2x-7)x0

Решаем последнее неравенство методом интервалов: на числовой прямой отмечаем все нули функции в левой части (это числа х = 2 и х = 4 для первой скобки, х = 3,5 - для второй и х = 0, но нули выкалываем, так как неравенство строгое).

Окончательно получаем: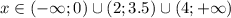 $x\in(-\infty; 0)\cup(2;3.5)\cup(4;+\infty)$ .