Решить показательное уравнение: 3*2^(x+1)-2^-(x)*5^(2x+1)=13*5^x Ребят решить пример​

Можно разделить обе части уравнения на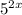 и выполнить замену 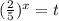, вы получите такое квадратное уравнение 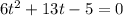далее самостоятельно решите. А так приведу решение графически.

График функции, стоящее слева в уравнении является убывающей как сумма двух убывающих функций. С прямой y = 5 имеет одну общую точку x = -1.

ответ: -1.

Решить показательное уравнение : 3*2ˣ⁺¹ - 2⁻ˣ*5²ˣ⁺¹ = 13*5ˣ

ответ:  -1 .

Объяснение:    3*2ˣ⁺¹ - 2⁻ˣ*5²ˣ⁺¹ =13*5ˣ ⇔ 6*2ˣ - 5*5²ˣ/2ˣ =13*5ˣ ⇔

6*(2ˣ)² -13*5ˣ*2ˣ  - 5*(5ˣ)² = 0    

* * * 6u² -13uv - 5v² =0  однородное уравнение второго порядка * * *

* * * 6*( (2/5)ˣ)² -13* (2/5)ˣ  -5 =0  * * *

2ˣ = (13*5ˣ ± √(169*5²ˣ +120*5²ˣ ) ) / ( 2*6)

2ˣ =(13*5ˣ  -17*5ˣ) /  12  = -(1/3)*5ˣ < 0            x∈∅

2ˣ =(13*5ˣ  +17*5ˣ) /  12  = (5 /2)*5ˣ   ⇔  (2/5)ˣ =(2/5) ⁻¹  

x = -1 .